Khan Academy on a Stick
Basic Trigonometry
-
 Basic trigonometry
cc
Basic trigonometry
ccIntroduction to trigonometry
-
 Example: Using soh cah toa
cc
Example: Using soh cah toa
ccWorked example evaluating sine and cosine using soh cah toa definition.
-
 Basic trigonometry II
cc
Basic trigonometry II
ccA few more examples using SOH CAH TOA
-
 Secant (sec), cosecant (csc) and cotangent (cot) example
cc
Secant (sec), cosecant (csc) and cotangent (cot) example
ccWorked example where we walk through finding the major trig ratios
-
 Example: Using trig to solve for missing information
cc
Example: Using trig to solve for missing information
ccWorked example using trig ratios to solve for missing information and evaluate other trig ratios
-
 Example: Calculator to evaluate a trig function
cc
Example: Calculator to evaluate a trig function
ccWorked example showing how to use typical calculators to evaluate trigonometric functions
-
 Example: Trig to solve the sides and angles of a right triangle
cc
Example: Trig to solve the sides and angles of a right triangle
ccWorked example using trigonometry to solve for the lengths of the sides of a right triangle given one of the non-right angles.
-
 Example: Solving a 30-60-90 triangle
cc
Example: Solving a 30-60-90 triangle
ccThis worked example can be done without trigonometry, but we do show how knowledge of 30-60-90 triangles can be helpful when evaluating trig functions
-
 Using Trig Functions
cc
Using Trig Functions
ccUsing Trigonometric functions to solve the sides of a right triangle
-
 Using Trig Functions Part II
cc
Using Trig Functions Part II
ccA couple of more examples of using Trig functions to solve the sides of a triangle.
Basic trigonometric ratios
In this tutorial, you will learn all the trigonometry that you are likely to remember in ten years (assuming you are a lazy non-curious, non-lifelong learner). But even in that non-ideal world where you forgot everything else, you'll be able to do more than you might expect with the concentrated knowledge you are about to get.
-
 Introduction to radians
cc
Introduction to radians
ccUnderstanding the definition and motivation for radians and the relationship between radians and degrees
-
 Radian and degree conversion practice
cc
Radian and degree conversion practice
ccA little practice converting between radians and degrees and vice versa
-
 Example: Radian measure and arc length
cc
Example: Radian measure and arc length
ccWorked example that thinks about the relationship between an arc length and the angle that is subtended by the arc.
-
 Example: Converting degrees to radians
cc
Example: Converting degrees to radians
ccWorked example to help understand how we covert radians to degrees
-
 Example: Converting radians to degrees
cc
Example: Converting radians to degrees
ccWorked example showing how to convert radians to degrees
-
 Radians and degrees
cc
Radians and degrees
ccWhat a radian is. Converting radians to degrees and vice versa.
Radians
Most people know that you can measure angles with degrees, but only exceptionally worldly people know that radians can be an exciting alternative. As you'll see, degrees are somewhat arbitrary (if we lived on a planet that took 600 days to orbit its star, we'd probably have 600 degrees in a full revolution). Radians are pure. Seriously, they are measuring the angle in terms of how long the arc that subtends them is (measured in radiuseseses). If that makes no sense, imagine measuring a bridge with car lengths. If that still doesn't make sense, watch this tutorial!
-
 Unit circle definition of trig functions
cc
Unit circle definition of trig functions
ccExtending SOH CAH TOA so that we can define trig functions for a broader class of angles
-
 Example: Unit circle definition of sin and cos
cc
Example: Unit circle definition of sin and cos
ccUnit circle definition to calculate sin and cos of multiple angles
-
 Example: Using the unit circle definition of trig functions
cc
Example: Using the unit circle definition of trig functions
ccWorked example using our knowledge of 30-60-90 triangles and similarity to evaluate tan, cos and sin.
-
 Example: Trig function values using unit circle definition
cc
Example: Trig function values using unit circle definition
ccWorked example that uses the unit circle definition to evaluate trig functions
-
 Example: The signs of sine and cosecant
cc
Example: The signs of sine and cosecant
ccUsing the unit circle definition to think out the sin and cosine of a negative angle.
Unit circle definition of trigonometric functions
You're beginning to outgrow SOH CAH TOA. It breaks down for angles greater than or equal to 90. It breaks down for negative angles. Sometimes in life, breaking a bad relationship early is good for both parties. Lucky for you, you don't have to stay lonely for long. We're about to introduce you to a much more robust way to define trigonometric functions. Don't want to get too hopeful, but this might be a keeper.
-
 Example: Graph, domain, and range of sine function
cc
Example: Graph, domain, and range of sine function
ccGraphing a sin curve to think about its domain and range.
-
 Example: Graph of cosine
cc
Example: Graph of cosine
ccBasic interpretation of the graph of the cosine function
-
 Example: Intersection of sine and cosine
Example: Intersection of sine and cosine
Thinking about where the graphs of sin and cos intersect.
-
 Example: Amplitude and period
cc
Example: Amplitude and period
ccDetermining the amplitude and period of a trig function
-
 Example: Amplitude and period transformations
cc
Example: Amplitude and period transformations
ccUnderstanding how the amplitude and period changes as coefficients change.
-
 Example: Amplitude and period cosine transformations
Example: Amplitude and period cosine transformations
Visualizing changes in amplitude and period for a cosine function
-
 Example: Figure out the trig function
cc
Example: Figure out the trig function
ccDetermining a trig function given its graph
-
 Graph of the sine function
cc
Graph of the sine function
ccUsing the unit circle definition of the sine function to make a graph of it.
-
 Graphs of trig functions
cc
Graphs of trig functions
ccExploring the graphs of trig functions
-
 Graphing trig functions
cc
Graphing trig functions
ccAnalyzing the amplitude and periods of the sine and cosine functions.
-
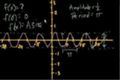 More trig graphs
cc
More trig graphs
ccDetermining the equations of trig functions by inspecting their graphs.
-
 Determining the equation of a trigonometric function
cc
Determining the equation of a trigonometric function
ccDetermining the amplitude and period of sine and cosine functions.
Graphs of trig functions
The unit circle definition allows us to define sine and cosine over all real numbers. Doesn't that make you curious what the graphs might look like? Well this tutorial will scratch that itch (and maybe a few others). Have fun.
-
 Inverse Trig Functions: Arcsin
cc
Inverse Trig Functions: Arcsin
ccIntroduction to the inverse trig function arcsin
-
 Inverse Trig Functions: Arccos
cc
Inverse Trig Functions: Arccos
ccUnderstanding the inverse cosine or arccos function
-
 Inverse Trig Functions: Arctan
cc
Inverse Trig Functions: Arctan
ccUnderstanding the arctan or inverse tangent function.
-
 Example: Calculator to evaluate inverse trig function
Example: Calculator to evaluate inverse trig function
Example using calculator to evaluate inverse tangent function
Inverse trig functions
Someone has taken the sine of an angle and got 0.85671 and they won't tell you what the angle is!!! You must know it! But how?!!! Inverse trig functions are here to save your day (they often go under the aliases arcsin, arccos, and arctan).
-
 Tau versus Pi
cc
Tau versus Pi
ccWhy Tau might be a better number to look at than Pi
Long live Tau
Pi (3.14159...) seems to get all of the attention in mathematics. On some level this is warranted. The ratio of the circumference of a circle to the diameter. Seems pretty pure. But what about the ratio of the circumference to the radius (which is two times pi and referred to as "tau")? Now that you know a bit of trigonometry, you'll discover in videos made by Sal and Vi that "tau" may be much more deserving of the throne!