Khan Academy on a Stick
Arithmetic properties
This tutorial will help us make sure we can go deep on arithmetic. We'll explore various ways to represent whole numbers, place value, order of operations, rounding and various other properties of arithmetic.
-
 Introduction to Order of Operations
cc
Introduction to Order of Operations
ccOrder of Operations
-
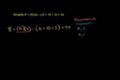 Order of Operations
cc
Order of Operations
ccOrder of Operations
-
 Order of Operations 1
cc
Order of Operations 1
ccOrder of Operations
-
 More Complicated Order of Operations Example
cc
More Complicated Order of Operations Example
ccMore Complicated Order of Operations Example
-
 Order of Operations examples
cc
Order of Operations examples
ccEvaluating expressions using order of operations
Order of operations
If you have the expression "3 + 4 x 5", do you add the 3 to the 4 first or multiply the 4 and 5 first? To clear up confusion here, the math world has defined which operation should get priority over others. This is super important. You won't really be able to do any involved math if you don't get this clear. But don't worry, this tutorial has your back.
-
 Place Value 1
cc
Place Value 1
ccPlace Value 1
-
 Place Value 2
cc
Place Value 2
ccPlace Value 2
-
 Place Value 3
cc
Place Value 3
ccPlace Value 3
Place value
You've been counting for a while now. It's second nature to go from "9" to "10" or "99" to "100", but what are you really doing when you add another digit? How do we represent so many numbers (really as many as we want) with only 10 number symbols (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)? In this tutorial you'll learn about place value. This is key to better understanding what you're really doing when you count, carry, regroup, multiply and divide with mult-digit numbers. If you really think about it, it might change your worldview forever!
-
 Rounding Whole Numbers 1
cc
Rounding Whole Numbers 1
ccRounding Whole Numbers 1
-
 Rounding Whole Numbers 2
cc
Rounding Whole Numbers 2
ccRounding Whole Numbers 2
-
 Rounding Whole Numbers 3
cc
Rounding Whole Numbers 3
ccRounding Whole Numbers 3
Rounding whole numbers
If you're looking to create an army of robot dogs, will it really make a difference if you have 10,300 dogs, 9,997 dogs or 10,005 dogs? Probably not. All you really care about is how many dogs you have to, say, the nearest thousand (10,000 dogs). In this tutorial, you'll learn about conventions for rounding whole numbers. Very useful when you might not need to (or cannot) be completely precise.
-
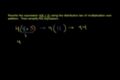 The Distributive Property
cc
The Distributive Property
ccThe Distributive Property
-
 The Distributive Property 2
cc
The Distributive Property 2
ccThe Distributive Property 2
-
 Distributive Property Example 1
cc
Distributive Property Example 1
ccck12 Distributive Property example
The distributive property
The distributive property is an idea that shows up over and over again in mathematics. It is the idea that 5 x (3 + 4) = (5 x 3) + (5 x 4). If that last statement made complete sense, no need to watch this tutorial. If it didn't or you don't know why it's true, then this tutorial might be a good way to pass the time :)
-
 Commutative Law of Addition
cc
Commutative Law of Addition
ccCommutative Law of Addition
-
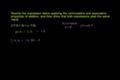 Commutative Property for Addition
cc
Commutative Property for Addition
ccCommutative Property for Addition
-
 Commutative Law of Multiplication
cc
Commutative Law of Multiplication
ccCommutative Law of Multiplication
-
 Associative Law of Addition
cc
Associative Law of Addition
ccAssociative Law of Addition
-
 Associative Law of Multiplication
cc
Associative Law of Multiplication
ccAssociative Law of Multiplication
-
 CA Algebra I: Number Properties and Absolute Value
cc
CA Algebra I: Number Properties and Absolute Value
cc1-7, number properties and absolute value equations
-
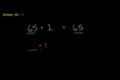 Identity Property of 1
cc
Identity Property of 1
ccIdentity Property of 1
-
 Identity property of 1 (second example)
cc
Identity property of 1 (second example)
ccIdentity property of 1
-
 Identity property of 0
cc
Identity property of 0
ccIdentity property of 0
-
 Inverse Property of Addition
cc
Inverse Property of Addition
ccThe simple idea that a number plus its negative is 0
-
 Inverse Property of Multiplication
cc
Inverse Property of Multiplication
ccSimple idea that multiplying by a numbers multiplicative inverse gets you back to one
Arithmetic properties
2 + 3 = 3 + 2, 6 x 4 = 4 x 6. Adding zero to a number does not change the number. Likewise, multiplying a number by 1 does not change it. You may already know these things from working through other tutorials, but some people (not us) like to give these properties names that sound far more complicated than the property themselves. This tutorial (which we're not a fan of), is here just in case you're asked to identify the "Commutative Law of Multiplication". We believe the important thing isn't the fancy label, but the underlying idea (which isn't that fancy).
Counting
How many times do you need to cut a cake? How many fence posts do you need? These life altering decisions will be based on how well you count.
Understanding whole number representations
Whether with words or numbers, we'll try to understand multiple ways of representing a whole number quantity. We'll even play with place value a good bit to make sure that everything is clicking!
 Counting 1 exercise
Counting 1 exercise Regrouping numbers intro various place values
Regrouping numbers intro various place values Comparing whole number place values
Comparing whole number place values Largest possible number from 4 digits example
Largest possible number from 4 digits example Recognizing irrational numbers
Recognizing irrational numbers