Khan Academy on a Stick
Exponents, radicals, and scientific notation
Understanding and solving exponents without algebra.
The world of exponents
Addition was nice. Multiplication was cooler. In the mood for a new operation that grows numbers even faster? Ever felt like expressing repeated multiplication with less writing? Ever wanted to describe how most things in the universe grow and shrink? Well, exponents are your answer! This tutorial covers everything from basic exponents to negative and fractional ones. It assumes you remember your multiplication, negative numbers and fractions.
-
 Understanding Square Roots
cc
Understanding Square Roots
ccUnderstanding Square Roots
-
 Approximating Square Roots
cc
Approximating Square Roots
ccApproximating Square Roots
-
 Simplifying square roots
Simplifying square roots
-
 Simplifying radicals
cc
Simplifying radicals
ccUsing exponent rules to simplify radicals or square roots
-
 Square Roots and Real Numbers
cc
Square Roots and Real Numbers
cc -
 Adding and simplifying radicals
cc
Adding and simplifying radicals
ccMore Simplifying Radical Expressions
The square root
A strong contender for coolest symbol in mathematics is the radical. What is it? How does it relate to exponents? How is the square root different than the cube root? How can I simplify, multiply and add these things? This tutorial assumes you know the basics of exponents and exponent properties and takes you through the radical world for radicals (and gives you some good practice along the way)!
-
 Finding Cube Roots
cc
Finding Cube Roots
ccFinding Cube Roots
-
 Cube root of a non-perfect cube
Cube root of a non-perfect cube
-
 Simplifying a cube root
cc
Simplifying a cube root
ccSimplifying Radical Expressions1
The cube root
If you're familiar with the idea of a square root, we're about to take things one step (dimension?) further with the cube root. This generally refers to finding a number that ,when cubed, is equal to the number that you're trying to find the cube root of!
-
 Patterns in zeros exercise
Patterns in zeros exercise
-
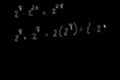 Exponent Rules Part 1
cc
Exponent Rules Part 1
ccIntroduction to exponent rules
-
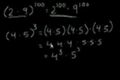 Exponent Rules Part 2
cc
Exponent Rules Part 2
cc2 more exponent rules with an introduction to composite problems
-
 Exponent Properties Involving Quotients
cc
Exponent Properties Involving Quotients
ccExponent Properties Involving Quotients
Exponent properties
Tired of hairy exponent expressions? Feel compelled to clean them up? Well, this tutorial might just give you the tools you need. If you know a bit about exponents, you'll learn a ton more in this tutorial as you learn about the rules for simplifying exponents.
-
 Introduction to scientific notation
cc
Introduction to scientific notation
ccIntroduction to scientific notation. An in-depth discussion about why and how scientific notation is used.
-
 Scientific Notation
cc
Scientific Notation
ccScientific Notation
-
 Scientific Notation Examples
cc
Scientific Notation Examples
ccMore scientific notation examples
-
 Scientific Notation I
cc
Scientific Notation I
ccScientific Notation I
-
 Scientific Notation Example 2
cc
Scientific Notation Example 2
ccScientific Notation 2
-
 Multiplying in Scientific Notation
Multiplying in Scientific Notation
u11_l1_t4_we_int Multiplying in Scientific Notation
-
 Multiplying in scientific notation example
cc
Multiplying in scientific notation example
ccMultiplying in scientific notation example
-
 Dividing in scientific notation example
cc
Dividing in scientific notation example
ccExample showing how to divide two numbers expressed in scientific notation
-
 Orders of magnitude exercise example 2
Orders of magnitude exercise example 2
Scientific notation
Scientists and engineers often have to deal with super huge (like 6,000,000,000,000,000,000,000) and super small numbers (like 0.0000000000532) . How can they do this without tiring their hands out? How can they look at a number and understand how large or small it is without counting the digits? The answer is to use scientific notation. If you come to this tutorial with a basic understanding of positive and negative exponents, it should leave you with a new appreciation for representing really huge and really small numbers!
-
 Negative exponents
Negative exponents
-
 Negative Exponent Intuition
cc
Negative Exponent Intuition
ccIntuition on why a^-b = 1/(a^b) (and why a^0 =1)
-
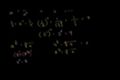 Zero, Negative, and Fractional Exponents
cc
Zero, Negative, and Fractional Exponents
ccZero, Negative, and Fractional Exponents
-
 Basic fractional exponents
Basic fractional exponents
-
 Negative fractional exponent examples
Negative fractional exponent examples
-
 Negative fractional exponent examples 2
Negative fractional exponent examples 2
-
 Fractional exponents with numerators other than 1
Fractional exponents with numerators other than 1
Negative and fractional exponents
It's normally a bad idea to hang around with negative people or do negative things, but we think it's OK to associate with negative exponents. And fractional exponents are even more fun. This idea will open up entirely new vistas to your mathematical life.
 Introduction to exponents
Introduction to exponents Raising a number to the 0th and 1st power
Raising a number to the 0th and 1st power Powers of 1 and -1
Powers of 1 and -1 Powers of fractions
Powers of fractions Powers of zero
Powers of zero Exponent example 1
Exponent example 1 Exponent example 2
Exponent example 2