Khan Academy on a Stick
Partial derivatives, gradient, divergence, curl
Thinking about forms of derivatives in multi-dimensions and for vector-valued functions: partial derivatives, gradient, divergence and curl.
-
Partial Derivatives
ccIntroduction to partial derivatives.
-
Partial Derivatives 2
ccMore on partial derivatives
Partial derivatives
Let's jump out of that boring (okay, it wasn't THAT boring) 2-D world into the exciting 3-D world that we all live and breath in. Instead of functions of x that can be visualized as lines, we can have functions of x and y that can be visualized as surfaces. But does the idea of a derivative still make sense? Of course it does! As long as you specify what direction you're going in. Welcome to the world of partial derivatives!
-
Gradient 1
ccIntroduction to the gradient
-
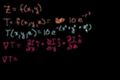Gradient of a scalar field
ccIntuition of the gradient of a scalar field (temperature in a room) in 3 dimensions.
Gradient
Ever walk on hill (or any wacky surface) and wonder which way would be the fastest way up (or down). Now you can figure this out exactly with the gradient.
-
Divergence 1
ccIntroduction to the divergence of a vector field.
-
Divergence 2
ccThe intuition of what the divergence of a vector field is.
-
Divergence 3
ccAnalyzing a vector field using its divergence.
Divergence
Is a vector field "coming together" or "drawing apart" at a given point in space. The divergence is a vector operator that gives us a scalar value at any point in a vector field. If it is positive, then we are diverging. Otherwise, we are converging!
Curl 1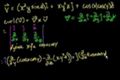
Curl 2
Curl 3