Khan Academy on a Stick
Line integrals and Green's theorem
Line integral of scalar and vector-valued functions. Green's theorem and 2-D divergence theorem.
-
 Introduction to the Line Integral
cc
Introduction to the Line Integral
ccIntroduction to the Line Integral
-
 Line Integral Example 1
cc
Line Integral Example 1
ccConcrete example using a line integral
-
 Line Integral Example 2 (part 1)
cc
Line Integral Example 2 (part 1)
ccLine integral over a closed path (part 1)
-
 Line Integral Example 2 (part 2)
cc
Line Integral Example 2 (part 2)
ccPart 2 of an example of taking a line integral over a closed path
Line integrals for scalar functions
With traditional integrals, our "path" was straight and linear (most of the time, we traversed the x-axis). Now we can explore taking integrals over any line or curve (called line integrals).
-
 Position Vector Valued Functions
cc
Position Vector Valued Functions
ccUsing a position vector valued function to describe a curve or path
-
 Derivative of a position vector valued function
cc
Derivative of a position vector valued function
ccVisualizing the derivative of a position vector valued function
-
 Differential of a vector valued function
cc
Differential of a vector valued function
ccUnderstanding the differential of a vector valued function
-
 Vector valued function derivative example
cc
Vector valued function derivative example
ccConcrete example of the derivative of a vector valued function to better understand what it means
Position vector functions and derivatives
In this tutorial, we will explore position vector functions and think about what it means to take a derivative of one. Very valuable for thinking about what it means to take a line integral along a path in a vector field (next tutorial).
-
 Line Integrals and Vector Fields
cc
Line Integrals and Vector Fields
ccUsing line integrals to find the work done on a particle moving through a vector field
-
 Using a line integral to find the work done by a vector field example
cc
Using a line integral to find the work done by a vector field example
ccUsing a line integral to find the work done by a vector field example
-
 Parametrization of a Reverse Path
cc
Parametrization of a Reverse Path
ccUnderstanding how to parametrize a reverse path for the same curve.
-
 Scalar Field Line Integral Independent of Path Direction
cc
Scalar Field Line Integral Independent of Path Direction
ccShowing that the line integral of a scalar field is independent of path direction
-
 Vector Field Line Integrals Dependent on Path Direction
cc
Vector Field Line Integrals Dependent on Path Direction
ccShowing that, unlike line integrals of scalar fields, line integrals over vector fields are path direction dependent
-
 Path Independence for Line Integrals
cc
Path Independence for Line Integrals
ccShowing that if a vector field is the gradient of a scalar field, then its line integral is path independent
-
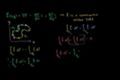 Closed Curve Line Integrals of Conservative Vector Fields
cc
Closed Curve Line Integrals of Conservative Vector Fields
ccShowing that the line integral along closed curves of conservative vector fields is zero
-
 Example of Closed Line Integral of Conservative Field
cc
Example of Closed Line Integral of Conservative Field
ccExample of taking a closed line integral of a conservative field
-
 Second Example of Line Integral of Conservative Vector Field
cc
Second Example of Line Integral of Conservative Vector Field
ccUsing path independence of a conservative vector field to solve a line integral
Line integrals in vector fields
You've done some work with line integral with scalar functions and you know something about parameterizing position-vector valued functions. In that case, welcome! You are now ready to explore a core tool math and physics: the line integral for vector fields. Need to know the work done as a mass is moved through a gravitational field. No sweat with line integrals.
-
 Green's Theorem Proof Part 1
cc
Green's Theorem Proof Part 1
ccPart 1 of the proof of Green's Theorem
-
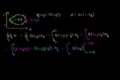 Green's Theorem Proof (part 2)
cc
Green's Theorem Proof (part 2)
ccPart 2 of the proof of Green's Theorem
-
 Green's Theorem Example 1
cc
Green's Theorem Example 1
ccUsing Green's Theorem to solve a line integral of a vector field
-
 Green's Theorem Example 2
cc
Green's Theorem Example 2
ccAnother example applying Green's Theorem
Green's theorem
It is sometimes easier to take a double integral (a particular double integral as we'll see) over a region and sometimes easier to take a line integral around the boundary. Green's theorem draws the connection between the two so we can go back and forth. This tutorial proves Green's theorem and then gives a few examples of using it. If you can take line integrals through vector fields, you're ready for Mr. Green.
-
 Constructing a unit normal vector to a curve
cc
Constructing a unit normal vector to a curve
ccFiguring out a unit normal vector at any point along a curve defined by a position vector function
-
 2 D Divergence Theorem
cc
2 D Divergence Theorem
ccUsing Green's Theorem to establish a two dimensional version of the Divergence Theorem
-
 Conceptual clarification for 2-D Divergence Theorem
cc
Conceptual clarification for 2-D Divergence Theorem
ccUnderstanding the line integral as flux through a boundary
2-D Divergence theorem
Using Green's theorem (which you should already be familiar with) to establish that the "flux" through the boundary of a region is equal to the double integral of the divergence over the region. We'll also talk about why this makes conceptual sense.