Khan Academy on a Stick
Indefinite and definite integrals
Indefinite integral as anti-derivative. Definite integral as area under a curve. Integration by parts. U-substitution. Trig substitution.
Indefinite integral as anti-derivative
You are very familiar with taking the derivative of a function. Now we are going to go the other way around--if I give you a derivative of a function, can you come up with a possible original function. In other words, we'll be taking the anti-derivative!
Riemann sums and definite integration
In this tutorial, we'll think about how we can find the area under a curve. We'll first approximate this with rectangles (and trapezoids)--generally called Riemann sums. We'll then think about find the exact area by having the number of rectangles approach infinity (they'll have infinitesimal widths) which we'll use the definite integral to denote.
Integration by parts
When we wanted to take the derivative of f(x)g(x) in differential calculus, we used the product rule. In this tutorial, we use the product rule to derive a powerful way to take the anti-derivative of a class of functions--integration by parts.
-
 U-substitution
cc
U-substitution
ccUsing U-substitution to find the anti-derivative of a function. Seeing that U-substitution is the inverse of the chain rule.
-
 U-substitution example 2
cc
U-substitution example 2
ccAnother example of using U-subsitution
-
 U-substitution Example 3
cc
U-substitution Example 3
ccManipulating the expression to make u-substitution a little more obvious.
-
 U-substitution with ln(x)
cc
U-substitution with ln(x)
ccDoing u-substitution with ln(x)
-
 Doing u-substitution twice (second time with w)
cc
Doing u-substitution twice (second time with w)
ccExample where we do substitution twice to get the integral into a reasonable form
-
 U-substitution and back substitution
U-substitution and back substitution
Using u-substitution and "back substituting" for x to simplify an expression
-
 U-substitution with definite integral
U-substitution with definite integral
Example of using u-substitution to evaluate a definite integral
-
 (2^ln x)/x Antiderivative Example
cc
(2^ln x)/x Antiderivative Example
ccFinding ∫(2^ln x)/x dx
-
 Another u-substitution example
cc
Another u-substitution example
ccFinding the antiderivative using u-substitution.
U-substitution
U-substitution is a must-have tool for any integrating arsenal (tools aren't normally put in arsenals, but that sounds better than toolkit). It is essentially the reverise chain rule. U-substitution is very useful for any integral where an expression is of the form g(f(x))f'(x)(and a few other cases). Over time, you'll be able to do these in your head without necessarily even explicitly substituting. Why the letter "u"? Well, it could have been anything, but this is the convention. I guess why not the letter "u" :)
-
 Riemann sums and integrals
Riemann sums and integrals
-
 Intuition for Second Fundamental Theorem of Calculus
Intuition for Second Fundamental Theorem of Calculus
-
 Evaluating simple definite integral
cc
Evaluating simple definite integral
cc -
 Definite integrals and negative area
Definite integrals and negative area
-
 Area between curves
Area between curves
-
 Area between curves with multiple boundaries
Area between curves with multiple boundaries
-
 Challenging definite integration
cc
Challenging definite integration
cc2010 IIT JEE Paper 1 Problem 52 Periodic Definite Integral. The second term at about minute 14 should have a positive sign. Luckily, it doesn't effect the final answer!
-
 Introduction to definite integrals
cc
Introduction to definite integrals
ccUsing the definite integral to solve for the area under a curve. Intuition on why the antiderivative is the same thing as the area under a curve.
-
 Definite integrals (part II)
cc
Definite integrals (part II)
ccMore on why the antiderivative and the area under a curve are essentially the same thing.
-
 Definite Integrals (area under a curve) (part III)
cc
Definite Integrals (area under a curve) (part III)
ccMore on why the antiderivative and the area under a curve are essentially the same thing.
-
 Definite Integrals (part 4)
cc
Definite Integrals (part 4)
ccExamples of using definite integrals to find the area under a curve
-
 Definite Integrals (part 5)
cc
Definite Integrals (part 5)
ccMore examples of using definite integrals to calculate the area between curves
-
 Definite integral with substitution
cc
Definite integral with substitution
ccSolving a definite integral with substitution (or the reverse chain rule)
Definite integrals
Until now, we have been viewing integrals as anti-derivatives. Now we explore them as the area under a curve between two boundaries (we will now construct definite integrals by defining the boundaries). This is the real meat of integral calculus!
-
 Introduction to trig substitution
cc
Introduction to trig substitution
cc -
 Another substitution with x=sin (theta)
Another substitution with x=sin (theta)
-
 Integrals: Trig Substitution 1
cc
Integrals: Trig Substitution 1
ccExample of using trig substitution to solve an indefinite integral
-
 Trig and U substitution together (part 1)
Trig and U substitution together (part 1)
-
 Trig and U substitution together (part 2)
Trig and U substitution together (part 2)
-
 Trig substitution with tangent
Trig substitution with tangent
-
 Integrals: Trig Substitution 2
cc
Integrals: Trig Substitution 2
ccAnother example of finding an anti-derivative using trigonometric substitution
-
 Integrals: Trig Substitution 3 (long problem)
cc
Integrals: Trig Substitution 3 (long problem)
ccExample using trig substitution (and trig identities) to solve an integral.
Trigonometric substitution
We will now do another substitution technique (the other was u-substitution) where we substitute variables with trig functions. This allows us to leverage some trigonometric identities to simplify the expression into one that it is easier to take the anti-derivative of.
Fundamental Theorem of Calculus
You get the general idea that taking a definite integral of a function is related to evaluating the antiderivative, but where did this connection come from. This tutorial focuses on the fundamental theorem of calculus which ties the ideas of integration and differentiation together. We'll explain what it is, give a proof and then show examples of taking derivatives of integrals where the Fundamental Theorem is directly applicable.
 Antiderivatives and indefinite integrals
Antiderivatives and indefinite integrals Indefinite integrals of x raised to a power
Indefinite integrals of x raised to a power Antiderivative of hairier expression
Antiderivative of hairier expression Basic trig and exponential antiderivatives
Basic trig and exponential antiderivatives Antiderivative of x^-1
Antiderivative of x^-1 Simple Riemann approximation using rectangles
Simple Riemann approximation using rectangles Generalizing a left Riemann sum with equally spaced rectangles
Generalizing a left Riemann sum with equally spaced rectangles Rectangular and trapezoidal Riemann approximations
Rectangular and trapezoidal Riemann approximations Trapezoidal approximation of area under curve
Trapezoidal approximation of area under curve Deriving integration by parts formula
Deriving integration by parts formula Antiderivative of xcosx using integration by parts
Antiderivative of xcosx using integration by parts Integral of ln x
Integral of ln x Integration by parts twice for antiderivative of (x^2)(e^x)
Integration by parts twice for antiderivative of (x^2)(e^x) Integration by parts of (e^x)(cos x)
Integration by parts of (e^x)(cos x) Fundamental theorem of calculus
Fundamental theorem of calculus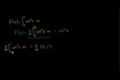 Applying the fundamental theorem of calculus
Applying the fundamental theorem of calculus Swapping the bounds for definite integral
Swapping the bounds for definite integral Both bounds being a function of x
Both bounds being a function of x Proof of Fundamental Theorem of Calculus
Proof of Fundamental Theorem of Calculus Connecting the first and second fundamental theorems of calculus
Connecting the first and second fundamental theorems of calculus Introduction to improper integrals
Introduction to improper integrals Improper integral with two infinite bounds
Improper integral with two infinite bounds Divergent improper integral
Divergent improper integral