Khan Academy on a Stick
First order differential equations
Differential equations with only first derivatives.
-
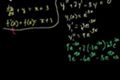What is a differential equation
ccWhat a differential equation is and some terminology.
-
Simple Differential Equations
cc3 basic differential equations that can be solved by taking the antiderivatives of both sides.
Intro to differential equations
How is a differential equation different from a regular one? Well, the solution is a function (or a class of functions), not a number. How do you like me now (that is what the differential equation would say in response to your shock)!
-
Separable Differential Equations
ccIntroduction to separable differential equations.
-
Separable differential equations 2
ccAnother separable differential equation example.
Separable equations
Arguably the 'easiest' class of differential equations. Here we use our powers of algebra to "separate" the y's from the x's on two different sides of the equation and then we just integrate!
-
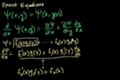Exact Equations Intuition 1 (proofy)
ccChain rule using partial derivatives (not a proof; more intuition).
-
Exact Equations Intuition 2 (proofy)
ccMore intuitive building blocks for exact equations.
-
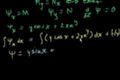Exact Equations Example 1
ccFirst example of solving an exact differential equation.
-
Exact Equations Example 2
ccSome more exact equation examples
-
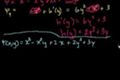Exact Equations Example 3
ccOne more exact equation example
-
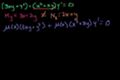Integrating factors 1
ccUsing an integrating factor to make a differential equation exact
-
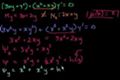Integrating factors 2
ccNow that we've made the equation exact, let's solve it!
Exact equations and integrating factors
A very special class of often non-linear differential equations. If you know a bit about partial derivatives, this tutorial will help you know how to 'exactly' solve these!
-
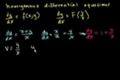First order homegenous equations
ccIntroduction to first order homogenous equations.
-
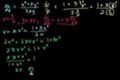First order homogeneous equations 2
ccAnother example of using substitution to solve a first order homogeneous differential equations.
Homogeneous equations
In this equations, all of the fat is fully mixed in so it doesn't collect at the top. No (that would be homogenized equations). Actually, the term "homogeneous" is way overused in differential equations. In this tutorial, we'll look at equations of the form y'=(F(y/x)).